| 央視網|中國網絡電視臺|網站地圖 |
| 客服設為首頁 |
中國網絡電視臺 >
| 首播 |
|
|
| 重播 |
|
|
唱片、齒輪、鸚鵡螺和數學家有什麼共同點?答案是他們都熱愛螺線。
 阿基米德螺線和三等分角
阿基米德螺線和三等分角
數學家對螺線的探索最早可以追溯到古希臘時代,阿基米德就在他的著作《論螺線》中對等速螺線的性質做了詳細的討論,於是後世的數學家們也把等速螺線稱為“阿基米德螺線”。(最早發現等角螺線的其實是阿基米德的老師柯農,在他死後阿基米德繼承了他的工作。)
什麼是阿基米德螺線呢?想象有一根可以繞著一點轉動的長桿,有一隻小蟲沿著桿勻速向外爬去。當長桿勻速轉動的時候小蟲畫出的軌跡就是阿基米德螺線。阿基米德螺線的方程寫成極坐標形式就是 ρ = aθ。
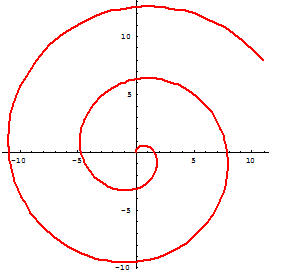
阿基米德螺線生活中隨處可見。在早期的留聲機中,電機帶動轉盤上的唱片勻速轉動,沿著一條直線軌道勻速向外圈移動的唱頭在唱片上留下的刻槽就是阿基米德螺線。同理,由勻速盤香機生産出來的盤狀蚊香也是阿基米德螺線的形狀。等螺距的螺釘從釘頭方向看去也是阿基米德螺線。就連縫紉機中也有阿基米德螺線出沒,一般的機械縫紉機中有一個凸輪,手輪旋轉的時候用來帶動縫紉針頭直線運動,這個凸輪的輪廓就是把阿基米德螺線的一部分經過對稱得到的。
一個很有趣的事情是,在阿基米德螺線的配合下,尺規就能完成三等分一個任意角θ。步驟如下:
1、將θ角的一邊與極軸重合,頂點與原點O重合2、延長角的另一邊與阿基米德螺線交于A3、尺規三等分OA得到三等分點B’、C’4、分別以OB’、OC’為半徑,O為圓心畫圓交螺線于B、C5、根據 ρ=aθ 容易證得OB、OC三等分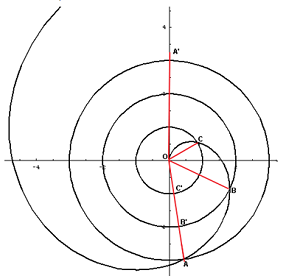
當然,只利用尺規是無法畫出阿基米德螺線的,所以我們大可不必擔心關於尺規三等分任意角不可能的證明就此被推倒。
漸開線和機械齒輪另一種有名的螺線叫做漸開線。當一根繩沿著另一曲線繞上或脫下時,它描出一條漸伸線。許多曲線都有自己的漸開線,把一條沒有彈性的細繩繞在一個定圓上,拉開繩子的一端並拉直,使繩子與圓周始終相切,繩子端點的軌跡就是圓的漸開線。
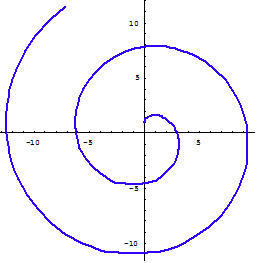
與阿基米德螺線相比,漸開線在日常生活中出場的機會似乎要少一點,但仔細尋找還是能發現它的蹤跡,例如棕櫚等一些植物葉尖的輪廓就是漸開線。其實它還在機械設備中發揮著重要的作用,機械設備用於傳動的齒輪中,就活躍著漸開線的身影。早在 1694 年,法國學者就討論了把漸開線作為齒輪齒形的可能性。 1765 年,歐拉對相嚙合的一對齒輪齒形曲線的曲率半徑和曲率中心位置的關係進行了計算,認為漸開線相當適合作為齒輪的齒形。與其他齒形相比,漸開線齒形具有傳動平穩、兩輪中心距允許有一定的安裝誤差等等優點。目前工業中漸開線齒輪被廣泛應用,佔到世界齒輪市場的 90% 以上。
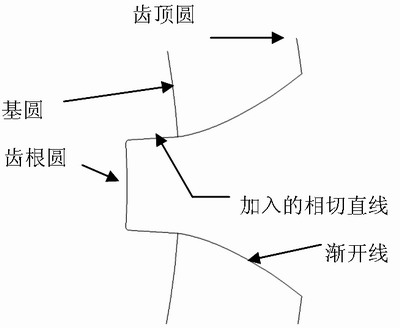
漸開線齒輪
伯努利和大自然都愛對角螺線下面出場的是螺線家族中名氣最大的——等角螺線。它的名字來源於一個著名的數學問題:試找出一條曲線,在任意點處的矢徑與切線的夾角為定值。這一問題最終於 1683 年被笛卡爾解決。使用一點簡單的微積分和笛卡爾的坐標係,我們很容易就能知道等角曲線的極坐標方程:ρ = e aθ 。由於在方程中出現了指數函數,這一螺線也被稱為對數螺線。
等角螺線還與一道著名的趣味物理題有關:三隻小狗分別從一個等邊三角形的三點出發,以相同的速度相互追逐,當它們在三角形中心相遇時,所畫出的軌跡就是等角螺線。一個很少被注意的有趣現象是,他們將在有限時間內相遇,但是相遇之前已經圍著中心繞了無數圈!
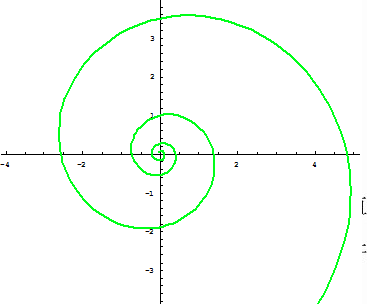
等角螺線
等角螺線具有許多有趣的數學性質,著名數學家雅各布�伯努利就是等角螺線的一個狂熱粉絲。他對等角螺線進行了許多研究,發現等角曲線在反演、求漸屈線、求垂足曲線、等比例放大等等變換後仍然是原先的等角曲線。對於這些性質伯努利感到十分驚訝,決定把等角曲線作為自己的墓誌銘,還加上了一句話“Eadem mutata resurgo.”這句話有各種不同的翻譯版本,大意是“縱然改變,仍然故我”(也有一些版本的翻譯類似“改變之後,我將原地復活”)。但是滑稽的是為他雕刻墓碑的工匠也許是文化水平不高,也許就是嫌麻煩,最後給墓碑上雕刻的圖竟是毫不相關的阿基米德螺線。伯努利若九泉有知,怕是要死不瞑目了。

等角對數螺線的除了伯努利還有大自然。可能是由於它等角的特性,等角螺線是自然界中最常見的螺線。向日葵的和其他一些植物的種子在花盤上排列出的曲線就是等角曲線,這樣每顆種子受到周圍其他種子所分泌生長素的抑製作用可以達到最小,同時當它們長大時可以保持形狀不變。蕨類植物和其他一些植物的嫩葉也蜷曲成對數曲線的形狀。

向日葵的花盤,能看出等角螺線嗎

對數曲線形狀的嫩芽
除了植物界,動物界也有不少等角螺線。鸚鵡螺的螺殼曲線就是等角螺線,這是由於鸚鵡螺在生長時內圈與外圈分泌石灰質的量總為一定值造成的,同理鷹嘴和鯊魚的背鰭也是對數螺線的形狀。法國博物學家,《昆蟲記》作者 讓-亨利 法布爾曾經注意到,蜘蛛結出的網上也有對數螺線出沒,對此他興趣大發,在《蜘蛛的一生》中增加了專門的一篇,討論對數螺線的數學性質和它對自然界的影響。甚至“對數螺線”這個名字就是法布爾叫響的。另外人們發現,飛蛾撲火與老鷹盤旋也都是沿著對數螺線的軌跡移動。
但是和接下來的銀河系相比,以上的例子都“弱爆了”。天文學家觀測發現,渦旋狀星雲的旋臂形狀與等角螺線十分相似,銀河系的四大旋臂就是傾斜度為 12� 的等角螺線。

其他的螺線
除此之外,數學家們還找出了各種奇形怪狀的非主流螺線,例如極坐標方程 r 2 = θ 描述的連鎖螺線,它不是常見的一支,而是對稱的兩支。更為怪異的是歐拉螺線,它有兩個中心,埃舍爾的一副作品就是以此為主題的。
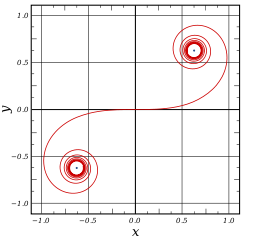
歐拉曲線
數學界是如此地熱愛螺線,以至於衡量一個數學家是否足夠牛逼的簡單的方法就是看看是否存在以他命名的螺線。那死理性派又為什麼對螺線情有獨鍾呢?這就正像法布爾總結的那樣:“幾何,以及面積的和諧支配著一切。”螺線背後精準優雅的規律,無疑讓一代又一代的人為之癡迷。
參考資料
【1】馬丁 加德納,《意料之外的絞刑和其他數學娛樂》
【2】 用數學註釋的花園
【3】趙文敏, 等角螺線及其他
【4】職業農夫, 生物中的數學---是生物因為數學而有趣?還是數學因為生物而有趣?
熱詞: