| 央視網|中國網絡電視臺|網站地圖 |
| 客服設為首頁 |
中國網絡電視臺 >
| 首播 |
|
|
| 重播 |
|
|

你會繫鞋帶嗎?這個問題似乎應該問幼兒園的小朋友。可是有的時候,繫鞋帶也是一項技術含量很高的工作,選出一種最好鞋帶係發並非易事。
啥樣的繫鞋帶的方法叫好呢?文藝小清新一定喜歡最靚、最帥的那款。可是死理性派則把這個問題看作一個優化問題:哪一種繫鞋帶的方法最節省鞋帶,所需要的鞋帶長度最短。
常見的鞋帶係法鞋帶穿過鞋孔的方法有千千萬萬,我們先只考慮比較常見的,就是鞋帶在左右鞋孔之間左一下、右一下來回穿梭的情況。
在查閱資料後,我們發現,符合上述説明的常規繫鞋帶方法有三種(如下圖):分別是美國式係法、歐洲式係法和鞋店式係法(也就是鞋店賣鞋的為了圖省事的一種簡單係法)。
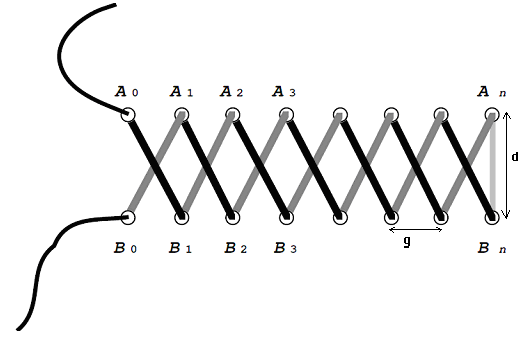
美國式係法
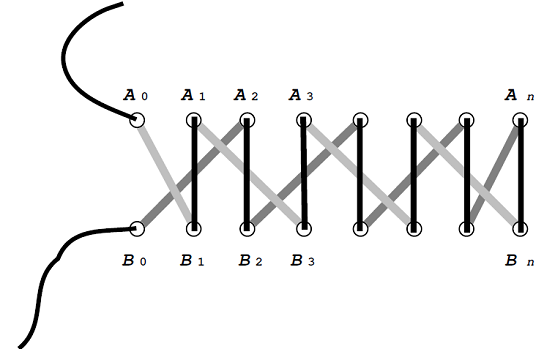
歐洲式係法
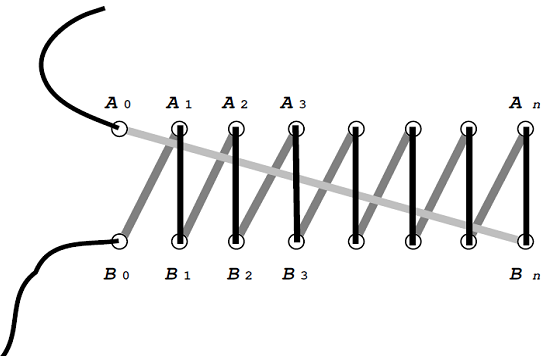
鞋店快速係法
這 3 種方法那一種更好呢?也就是説,哪種係法最省鞋帶呢?
不妨然我們先來確定這個“鞋帶工程”涉及到了哪些變量:
鞋上一共有多少對鞋孔:n:相鄰兩個鞋孔之間的距離:d左面那一行鞋孔和右邊那一行鞋孔的距離:g根據勾股定理和一些簡單的幾何知識,我們可以很輕鬆的算出這 3 種繫鞋帶方法所需要的鞋帶長度(只考慮穿過鞋孔的長度,不考慮係蝴蝶結所需要的長度)分別為:
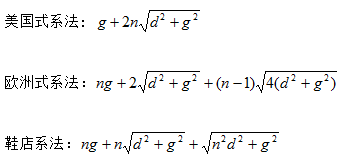
在 n, d, g 的值不同的情況下,這 3 個函數哪一個最大呢?選幾個數帶進去算算就知道了。假設鞋有 8 對鞋孔( n = 8 ),鞋孔間距離是 1 厘米( d = 1 ),左右鞋孔間的距離是 2 厘米( g = 2 ),這 3 種係法所需要的鞋帶長度分別是:
美國式係法:38厘米歐洲式係法:40厘米鞋店係法:42厘米如果按照一條 60 厘米的鞋帶的價格 1 元算的話,採用美國式係法可以比第 3 種係法為你節省一大筆錢:人民幣 0.07 元。再試試其他型號的鞋子,幾乎每次都是美國式係法都可以擊敗另外兩種係法,美國式係法似乎應該是 3 種之中是最好的,那是不是在所有的係法中它都是最好的呢?
最優鞋帶係法和光線傳播之間的聯絡其實,這個問題和光線反射與折射問題有著很巧妙的聯絡。光在傳播的時候有個“怪癖”,總是“抄近道”,選擇走最短的路徑(當然,死理性派知道這種説法是不嚴謹的,詳情請看 獻給業餘數學之王:澄清對費馬原理的誤解 )。我們就知道光的入射角等於反射角,但是可能很少人想過這個現象背後更深層的原因:因為只有這樣,才可以保證光線總能以最短的路徑達到目的地。比如下面的圖中,A點在入射光線上,B點在反射光線上,AB兩點之間相當於有一條直線連接,“兩點之間,線段最短”,如果入射角不等反射角,經過AB兩點的光線就未必可以保證走的路最短。

回到鞋帶的問題上,鞋帶在兩排鞋孔之間來回穿梭相當於光線在兩面相對的鏡子之間反射來反射去。而美國式係法恰好相當於光線以入射角等於反射角的方式進行來回反射(第 n 個鞋孔除外),自然保證了是三種方式中最省鞋帶,也是所有可能方式中距離最短的繫鞋帶方法。
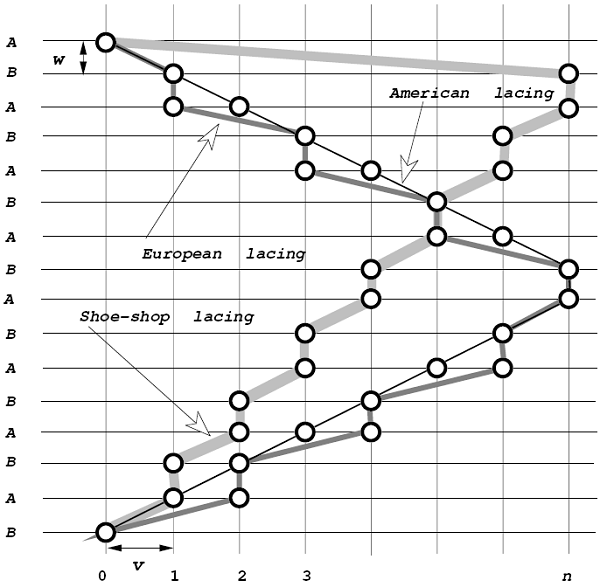
在下面的這幅圖裏,每一條橫線交替代表左邊的一行鞋孔( A )和右邊 ( B )一行鞋孔,豎線代表第 1,2,3,……n 個鞋孔。我們可以在一個平面上清楚地看到這三種鞋帶係法是怎樣穿過所有的鞋孔的。美國式係法幾乎是直線,而另外兩種係法曲曲折折,走的距離長也就不出乎意料了。
 更省鞋帶的非主流係法
更省鞋帶的非主流係法
看到這裡你可能會問,是誰這麼閒研究了這樣讓人想不到的問題?其實以上的繫鞋帶指南出自一篇論文,下圖是這篇奇特的論文的作者,美國北卡羅萊納大學的 John H. Halton 大叔。

雖然我們簡單介紹了這篇論文的內容,不過故事還沒有完,剛剛説的最短係法只是在鞋帶每次都是在左右鞋孔之間來回穿梭的假設之下的。事實上,在 John 發表論文之後,就有人開始提出異議,認為如果扔掉這個假設,還有比美國式係法更短的係法,比如下面的這個係法:
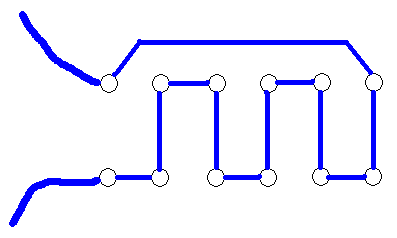
如果 n 是偶數,需要的鞋帶長度只有 ( n – 1 )( g + 2d ) 。據説加拿大皇家海軍和皇家空軍曾用這種方式繫鞋帶,原因倒不是為了節省鞋帶,而是鞋帶很容易從中間用刀一下子劃開,這樣在遇到危急情況,比如溺水的時候,便於脫掉鞋子逃生。
看來,繫鞋帶這件技術活也不是那麼容易的。
原來繫鞋帶的學問這麼大!幸好我穿的鞋不用繫鞋帶……參考資料:
The shoelace problem, H Halton - Mathematical Intelligencer, 1995How to Cut a Cake: And Other Mathematical Conundrums, Ian Stewart
熱詞: