| 央視網|中國網絡電視臺|網站地圖 |
| 客服設為首頁 |
中國網絡電視臺 >
| 首播 |
|
|
| 重播 |
|
|

警察在處理案子時總會遇到許多難題,其中之一就是根據犯罪現場的蛛絲馬跡還原出兇手作案時的完整情況。他們要從海量的干擾信息中篩選出對案件有幫助的,再通過分析這些信息推斷出正確的結論。
這正是數學拯救世界的時刻。從現場測得的數據可以使用小波、概率論和統計學等方法進行儲存與解讀。對於警察來説,數學最重要的功能是通過對數據的各種變換處理,一舉找到真正有用的信息。根據對現場數據的分析,警方往往要逆向地還原出案發時的場景,確定誰才是嫌疑犯。這個要倒過來的過程,在數學上被稱為反問題。接下來我們就通過列舉幾個實例來展示數學是如何在偵查領域立下戰功的。
算出車禍時的汽車行駛速度
交通事故可謂是世界上最頻發的案件,而案發時的車速則是衡量事故責任的重要依據之一。
一般來説,警察在交通事故現場能夠獲得的信息不外乎車輛被損壞的程度、目擊者描述以及車胎的印記。但倘若沒人看到,誰來判斷這是意外車禍還是蓄意謀殺?但如果車主真的踩了剎車(也就是意外車禍),輪胎痕跡是不會説謊的。通常“踩過剎車”的輪胎痕跡應該呈現一個“三段式”的特徵:
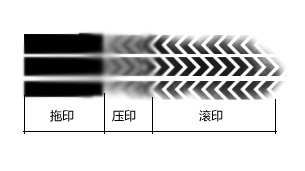
通過前後輪胎痕判斷軸距(示意圖)
滾印-壓印-拖印。由於汽車的制動力是逐漸加強的,所以在司機踩下制動的時候,胎痕首先會從滾印變成壓印,而後車胎“抱死”,拖印也就在這個時候出現了。因此,只要測量壓印和拖印出現的時間和特徵,就可以很輕易地得知汽車是否剎車,以及是何時開始剎車的了。這個問題謀殺站曾在 意外車禍還是蓄意謀殺?輪胎痕跡不説謊! 中有過詳細討論。
如果我們只關心車速,那只要測出制動拖印長度(即剎車距離)和地面的摩擦系數,就可以請出牛頓經典力學登場解決問題了。也許這是一個高中生都會做的物理題,但它的確在事故調查中發揮了很大作用。
實際中,交警的估算要複雜很多,比如剎車過程中,摩擦系數(實際中稱為附著系數)會隨著汽車制動的過程而發生變化,這時就需要大量的實踐總結,用一個可靠的經驗公式來修正。而如果事故是發生在積水較深的路面上,積水的影響則不容忽視(水滑現象),這時候的計算則需要引入水壓強以及水和胎面間迎擊面長度這些變量。
還原歹徒車牌號碼“緊急!緊急!城南方向有一家珠寶店被搶劫了!”大家紛紛武裝到牙齒,摩拳擦掌,準備去和歹徒搏鬥。可是等等,哪輛車才是歹徒駕駛的?
好消息是攝像頭拍下了汽車逃逸時的畫面。
壞消息是那個畫面看不清楚。

別擔心,這時候數學又大顯神威了。我們可以認為,看不清的圖像就是清晰圖像經過“模糊”過程後得到的結果。用數學的話來説就是,“模糊”可以看做是一個函數。只要我們能夠知道這個函數的表達式,就可以設法逆向地還原出清晰的圖像。我們同樣可以用函數來表示清晰圖像與模糊圖像,分別記為 f 和 h ,而把模糊過程記為 g。那麼一般而言,這個模糊過程的模型就是如下這樣:
在上式中,x 表示任意一個像素, f( x ) 是清晰圖像中每個像素的圖像, h( x ) 就是模糊圖像中每個像素的圖像。如果我們能夠知道 g( y ) 的詳細情況(這可以根據汽車的實際運動情況模擬得出),那麼便能夠通過 h( x ) 解出 f( x )。下圖是用數學方法得到的清晰圖像與抓住歹徒後拍攝的真實圖像,是不是感到還原度非常高呢?

 從算出連環殺手的住處到確定傳染病的傳染源
從算出連環殺手的住處到確定傳染病的傳染源
連環殺人犯總讓人都感到恐慌,尤其是當你和他同處一城的時候。如何根據已有的犯罪地點、時間等數據,推測出兇手的家在哪?
在美劇 《NUMB3RS》 的第一集裏就出現了這樣的情節。然而與一般警局不同的是,他們請來了一位數學家,這位數學家就使用了犯罪地理學中如下的公式,計算出了連環殺手可能的住處。
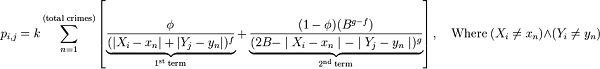
其中 | X i - x n | + | Y i - y n | 表示的是點 ( X i , Y i ) 到第 n 個犯罪地點 ( x n , y n ) 的 曼哈頓距離 。其中還有三個常數 f , g , k ,則大概是經驗數據或由計算機擬合得到的。這個公式計算出來的 p i,j 就表示犯罪住處位於 ( X i , Y i ) 的概率。

這麼一大塊公式看起來很神奇,它是怎麼得到的?實際上,通過對犯罪心理學的研究,數學家發現犯罪分子在作案時有兩個比較明顯的特徵:
1.考慮到成本,便捷性以及對周圍環境的熟悉,他們不會在離自己住所太遠的地方作案——實際上 70% 的連環殺人犯都會在離住所兩英里內的區域作案.
2.為了安全起見,不留下讓警察懷疑到自己的蛛絲馬跡,連環殺人犯也不會貿然對自己的鄰居下手。
上述的公式就是在這樣的大框架內得出來的,並且在實際運用中效果也很不錯。
有趣的是,這個本用來抓捕犯人的數學公式竟然還能用到對傳染病的控制上!衛生部門希望在傳染病剛剛流行的時候就能夠找到傳染病的源頭,從而在造成更大影響之前將其撲滅。巧合的是,傳染病的傳播特徵和罪犯選擇作案地點的特徵非常相似。無論是什麼樣的傳染病,都需要生活在寄主體內,基本不可能在空氣中長久地漂浮,所以它們不會感染離源頭太遠的地方。又因為傳染病源不能百分百保證感染遇見的每一個寄主,所以它們需要從源頭擴散到一定的距離才能找到適合生存的新環境——“不能太遠也不能太近”,這和連環殺手的作案風格如出一轍。在這裡,數學又一次出人意料地在看起來不相關的領域大展拳腳。
本文對一些現代的數學破案方法做了一個概括的介紹,但沒有詳細地解釋具體細節。這是因為現實中涉案的諸多因素都很複雜,並且絕大多數情況下這些方法需要借助計算機模擬,並非一兩段話就能夠説明詳情。
熱詞: