| 央視網|中國網絡電視臺|網站地圖 |
| 客服設為首頁 |
中國網絡電視臺 >
| 首播 |
|
|
| 重播 |
|
|
近日,連線網站評出了 9 大 Geek 不可不知(至少假裝知道)的公式。但這些公式大多數人難有機會用到,所以光知道幾個式子實在沒什麼意思。好在它們是如此強大,以至於每個都有許多精彩故事和神奇用途,比如有公式甚至能算出你有多漂亮。死理性派從中選擇了幾個最有意思的,講述那些神奇的故事。或許看完你還是不會用這些公式,但至少也能説得頭頭是道了。
歐拉公式
所有沒有歐拉公式的公式排行榜都是不專業的,即便死理性派對歐拉公式的 介紹 已經 夠多夠多 了,在這裡依然不敢抹去它。讓我們再次看看它是怎樣用三個最基礎的運算,把數學中最神奇的三個常數以及最根本的兩個數聯絡在一起的吧。
麥克斯韋方程

如果沒有麥克斯韋方程,現在我們在郵局看到的可能還是一排排的鴿籠。而至於上微博、發短信這樣的事情更是想無可想。因此也有人評論説,麥克斯韋對基礎自然科學的貢獻僅次於牛頓和愛因斯坦。
這個著名的方程組共有四個方程,分別是:高斯定律(描述電荷如何産生電場)、高斯磁定律(論述磁單極子不存在)、法拉第感應定律(時變磁場産生電場)和麥克斯韋—安培定律(電流和時變電場産生磁場)。
1865 年,麥克斯韋在他的論文中首次提出麥克斯韋方程組的概念,並預言了電磁波的存在,推導出電磁波的速度與光速相同(他甚至還預言了光是電磁波的一種)。麥克斯韋方程優美的特性和簡潔的表述讓年輕的赫茲堅信麥克斯韋關於電磁波的預言是正確的,在麥克斯韋去世 9 年後( 1888 年),赫茲終於通過實驗證實了電磁波的存在。他在實驗中甚至觀測到光電效應,但只是記錄下了這一現象,並未深入研究。 1895 年,意大利人馬可尼發明了無線電報並將其商用,書面信息終於可以不依靠(傳統意義上的)物質載體而存在,並能夠以光速瞬時傳遍全球。
根據方程組第二個方程,即高斯磁定律,物理學家們推斷出磁單極子是不存在的。我們知道,磁鐵都有 N 和 S 兩極,如果將磁鐵從中間截斷,兩塊新磁鐵也各有兩極。那麼存在只有一極的物質嗎?在弦理論中,將這樣的基本粒子稱為磁單極子,狄拉克在 1931 年首次預測了磁單極子存在的條件,大統一理論也需要磁單極子的存在作為基礎。遺憾的是,直到目前為止並沒有證明磁單極子存在的直接證據。在《生活大爆炸》第二季中,謝耳朵和他的朋友們前往北極就是為了尋找磁單極子存在的證據。如果磁單極子真的存在的話,那麼麥克斯韋方程組的第二個和第三個方程都要相應地修正。
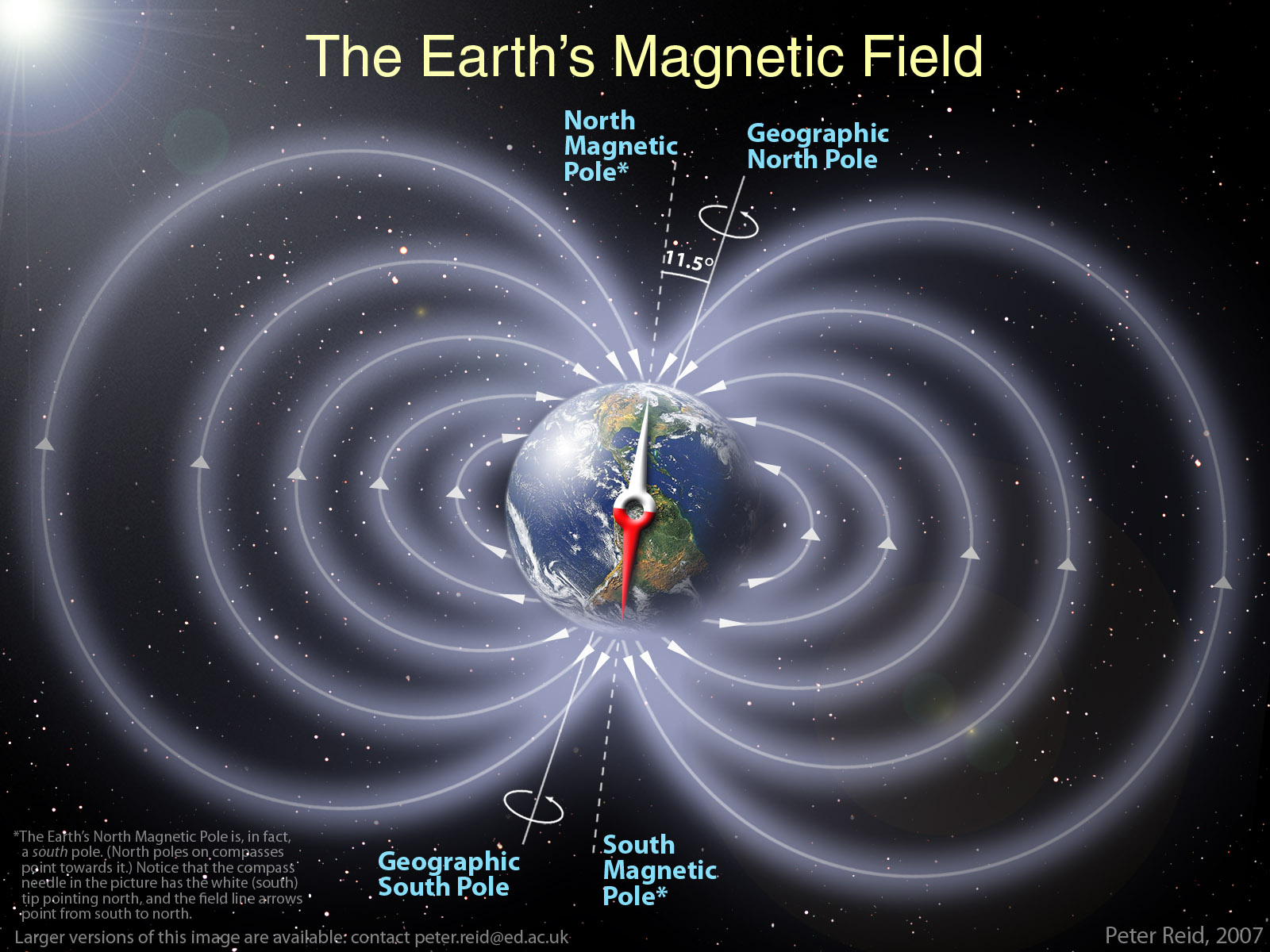
地球磁極,圖片來源:blogspot.com
薛定諤方程
1900 年,物理學界一片歌舞昇平,開爾文男爵在一場講演中説,物理學將不會再有任何發現,剩下的只是精益求精的測量。但他同時也指出,在物理學的晴空中還飄着兩朵小烏雲——以太風的觀測失敗(後來證明以太事實上不存在)和黑體輻射公式的紫外災難。但正是這兩朵小烏雲,徹底顛覆了傳統物理學,並催生出 20 世紀物理學的兩個最重要的主題——相對論和量子力學。而維也納物理學家薛定諤提出的薛定諤方程則是量子力學領域的基礎性理論之一:

其中 Ψ 是波函數,而|Ψ|^2就表示一個粒子在空間 x 和時間 t 出現的概率,這在經典物理中是不可想象的,一個粒子在要麼在這裡要麼在那裏,怎麼會以概率的方式出現?就連薛定諤本人在提出這個方程時也對 Ψ 的含義也不甚了了, 1927 年波爾和海森堡提出了哥本哈根詮釋(注意,這只是一個“詮釋”),認為 Ψ 表示波函數,並引入概率的概念,成功地解釋了薛定諤方程。但薛定諤始終也無法接受這樣的解釋,他用思想實驗“薛定諤的貓”來歸謬:一隻貓怎麼可能隨時死去活來?而愛因斯坦對哥本哈根詮釋的評價更直接:“上帝不擲骰子!”
要説的是,薛定諤提出該方程時已經將近 40 歲,也算是大器晚成的科學家。根據 野史 的説法,法國“官二代”德布洛意玩票去讀了物理博士,臨近畢業時毫無建樹,聽説愛因斯坦和普朗克弄出了一個叫做“光的波粒二象性”的時髦説法,一拍腦門寫了一篇只有 1 頁多的博士論文,稱任何物質都有波粒二象性。但學術委員會也不是吃素的,這樣的論文怎能通過教授們的法眼?但德布洛意的導師郎之萬將這篇論文寄給了愛因斯坦,愛因斯坦客氣地回信説此想法很有新意云云,這讓德布洛意順利過關。按照慣例,這篇論文被寄送到歐洲各個大學,在蘇黎世大學,學霸德拜將這篇論文交給默默無聞的薛定諤講師,讓他在兩周之後的討論班給大家講講。薛定諤看得雲裏霧裏自然也講得一塌糊塗,德拜聽後不甚滿意,卻沒有直接批評薛定諤,隨口説到,既然物質都是波,那總要有個波動方程吧?薛定諤靈光一現,就寫出了震驚學界的薛定諤方程。

參加第五屆索爾維會議的物理學家合影,點 這裡 查看高清大圖
上面的話雖有玩笑成分,但也並非都是戲説。實際上,德布洛意的確是個“官二代”,他提出了德布洛意波的概念,因此受到愛因斯坦的讚賞,薛定諤也正是受這篇論文的啟發提出薛定諤方程。但其他都是小説家的演繹。德布洛意在讀期間至少發表了 5 篇論文,他的博士論文長達 100 多頁,有興趣研究的同學可以在這裡 閱讀到 。
基本傳染數 R0
除了晦澀的物理方程,下面要介紹的兩個內容就沒有那麼抽象了,基本傳染數 R0 就是其中之一。
在傳染病學中,假設一個種群是封閉的(沒有遷入和遷出的個體),並且沒有免疫力,那麼某個個體感染疾病後,他能傳染的平均個體數就被稱作基本傳染數 R0 。
一般來説,如果 R0 < 1,傳染病就會逐漸消失,這也符合直觀的想象。但如果 R0 > 1,那傳染病就會以指數的方式爆發(由於患病的個體可能會死亡,加之種群數有限,所以最終的傳播速度會顯著下降)。
確定 R0 的數值對於傳染病防疫決策有着重要的作用,例如香港中文大學的研究顯示,2003 年爆發的 SARS 的 R0 指數在強力的防控措施下大約是 0.85,在沒有控制的情況下為 2 ~ 3,可見有效的防控措施對於控制疫情發展有着重要的作用。根據 維基百科 的資料,常見的傳染病的 R0 指數為:
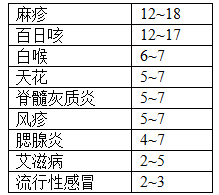
另外,在人口學中, R0 有時也被解釋為一個個體平均繁衍的後代的個數。
但由於多方面的原因, R0 一般很難直接由觀測得到。所以一個常見的方法是建立傳染病的微分方程模型,利用數學推導的方法得到 R0 的數值。但這種方法也有一定的缺陷,主要是因為數學模型本身就是一個簡化模型,特別是當存在交叉感染時,即便是定性的微分方程分析也相當具有挑戰性。而且有時利用數學模型得到的 R0 儘管可以預測傳染病是否能夠爆發,但與傳統意義上的平均傳染數仍然不同。關於如何利用數學模型來研究實驗中不易測量的參數也是目前交叉科學的熱門課題之一,這裡就不詳述了。
回到傳染病學的概念,那麼在 R0 = 1 時,疾病會不會爆發呢?一般來説我們不關心這樣的情況,因為往往這個狀態都是不穩定的,只要有微小的擾動就能變成一個確定的不等式。如果非要刨根問底,或許只有薛定諤的貓(如果它還活着的話)才能回答這個問題了……
計算你有多漂亮的公式
儘管將一切都量化聽起來十分美妙,但將人類的審美完全量化聽起來仍然像天方夜譚。退一步講,即使有了將審美量化的方法,仍然無法保證這樣的“美”是每個人都能欣賞的。
最近以色列的研究人員提出了 一種算法 來研究“最具吸引力的臉龐”。這個算法利用計算機分析經過預先打分的人類面部圖像。計算機學習這些數據後,就能夠為新的面部圖像進行吸引力評分。
他們的理論基礎是,近年來的研究顯示,人類面部的吸引力是超越種族、國家和文化的,因此應當存在普適性的(面部)審美標準。研究人員利用下面的公式進行回歸分析:
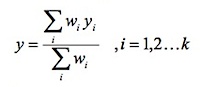
其中 y 是某個圖像的分數, y i 是臨近的圖像,而 w i 則是對應的權重。經過實測,利用該算法為面部圖像打分的結果與人類打分的結果最高有 0.65 的相關性。儘管這一數字還不夠理想,但仍然提供了一個新的研究方向。

各個分數段的標準長相,圖片來源:wired.com
如果有朝一日真的能將審美量化的話,由此導致的千篇一律的人造美女會不會帶來審美疲勞?當真如此的話,這個算法是否應當還需要考慮減去審美疲勞帶來的負面作用呢?
參考資料: 9 Equations True Geeks Should (at Least Pretend to) Know
熱詞: