圓周率π的計算歷程

央視國際 2004年06月23日 16:31

　　圓周率是一個極其馳名的數。從有文字記載的歷史開始，這個數就引進了外行人和學者們的興趣。作為一個非常重要的常數，圓周率最早是出於解決有關圓的計算問題。僅憑這一點，求出它的儘量準確的近似值，就是一個極其迫切的問題了。事實也是如此，幾千年來作為數學家們的奮鬥目標，古今中外一代一代的數學家為此獻出了自己的智慧和勞動。回顧歷史，人類對 π 的認識過程，反映了數學和計算技術發展情形的一個側面。 π 的研究，在一定程度上反映這個地區或時代的數學水平。德國數學史家康托説：“歷史上一個國家所算得的圓周率的準確程度，可以作為衡量這個國家當時數學發展水平的指標。”直到19世紀初，求圓周率的值應該説是數學中的頭號難題。為求得圓周率的值，人類走過了漫長而曲折的道路，它的歷史是饒有趣味的。我們可以將這一計算歷程分為幾個階段。

　　實驗時期

　　通過實驗對 π 值進行估算，這是計算 π 的第一階段。這種對 π 值的估算基本上都是以觀察或實驗為根據，是基於對一個圓的周長和直徑的實際測量而得出的。在古代世界，實際上長期使用 π ＝3這個數值。最早見於文字記載的有基督教《聖經》中的章節，其上取圓周率為3。這一段描述的事大約發生在公元前950年前後。其他如巴比倫、印度、中國等也長期使用3這個粗略而簡單實用的數值。在我國劉徽之前“圓徑一而週三”曾廣泛流傳。我國第一部《周髀算經》中，就記載有圓“週三徑一”這一結論。在我國，木工師傅有兩句從古流傳下來的口訣：叫做：“週三徑一，方五斜七”，意思是説，直徑為1的圓，周長大約是3，邊長為5的正方形，對角線之長約為7。這正反映了早期人們對圓周率 π 和√2 這兩個無理數的粗略估計。東漢時期官方還明文規定圓周率取3為計算面積的標準。後人稱之為“古率”。

　　早期的人們還使用了其它的粗糙方法。如古埃及、古希臘人曾用谷粒擺在圓形上，以數粒數與方形對比的方法取得數值。或用勻重木板鋸成圓形和方形以秤量對比取值……由此，得到圓周率的稍好些的值。如古埃及人應用了約四千年的 4 (8/9)2 = 3.1605。在印度，公元前六世紀，曾取 π= √10 = 3.162。在我國東、西漢之交，新朝王莽令劉歆製造量的容器——律嘉量斛。劉歆在製造標準容器的過程中就需要用到圓周率的值。為此，他大約也是通過做實驗，得到一些關於圓周率的並不劃一的近似值。現在根據銘文推算，其計算值分別取為3.1547，3.1992，3.1498，3.2031比徑一週三的古率已有所進步。人類的這種探索的結果，當主要估計圓田面積時，對生産沒有太大影響，但以此來製造器皿或其它計算就不合適了。

　　幾何法時期

　　憑直觀推測或實物度量，來計算 π 值的實驗方法所得到的結果是相當粗略的。

　　真正使圓周率計算建立在科學的基礎上，首先應歸功於阿基米德。他是科學地研究這一常數的第一個人，是他首先提出了一種能夠借助數學過程而不是通過測量的、能夠把 π 的值精確到任意精度的方法。由此，開創了圓周率計算的第二階段。

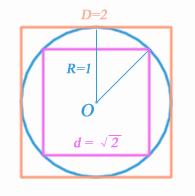
	圓周長大於內接正四邊形而小于外切正四邊形，因此 2√2 ＜ π ＜ 4 。當然，這是一個差勁透頂的例子。據説阿基米德用到了正96邊形才算出他的值域。

　　阿基米德求圓周率的更精確近似值的方法，體現在他的一篇論文《圓的測定》之中。在這一書中，阿基米德第一次創用上、下界來確定 π 的近似值，他用幾何方法證明了“圓周長與圓直徑之比小于 3+(1/7) 而大於 3 + (10/71) ”，他還提供了誤差的估計。重要的是，這種方法從理論上而言，能夠求得圓周率的更準確的值。到公元150年左右，希臘天文學家托勒密得出 π ＝3.1416，取得了自阿基米德以來的巨大進步。

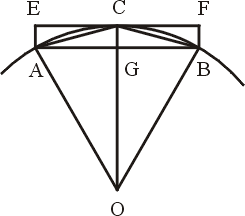
	割圓術。不斷地利用勾股定理，來計算正N邊形的邊長。

　　在我國，首先是由數學家劉徽得出較精確的圓周率。公元263年前後，劉徽提出著名的割圓術，得出 π ＝3.14，通常稱為“徽率”，他指出這是不足近似值。雖然他提出割圓術的時間比阿基米德晚一些，但其方法確有著較阿基米德方法更美妙之處。割圓術僅用內接正多邊形就確定出了圓周率的上、下界，比阿基米德用內接同時又用外切正多邊形簡捷得多。另外，有人認為在割圓術中劉徽提供了一種絕妙的精加工辦法，以至於他將割到192邊形的幾個粗糙的近似值通過簡單的加權平均，竟然獲得具有4位有效數字的圓周率 π ＝3927/1250 ＝3.1416。而這一結果，正如劉徽本人指出的，如果通過割圓計算得出這個結果，需要割到3072邊形。這種精加工方法的效果是奇妙的。這一神奇的精加工技術是割圓術中最為精彩的部分，令人遺憾的是，由於人們對它缺乏理解而被長期埋沒了。

　　恐怕大家更加熟悉的是祖衝之所做出的貢獻吧。對此，《隋書律曆志》有如下記載：“宋末，南徐州從事祖衝之更開密法。以圓徑一億為丈，圓周盈數三丈一尺四寸一分五厘九毫二秒七忽，朒數三丈一尺四寸一分五厘九毫二秒六忽，正數在盈朒二限之間。密率：圓徑一百一十三，圓週三百五十五。約率，圓徑七，週二十二。”

　　這一記錄指出，祖衝之關於圓周率的兩大貢獻。其一是求得圓周率

　　3.1415926 ＜ π ＜ 3.1415927

　　其二是，得到 π 的兩個近似分數即：約率為22／7；密率為355／113。

　　他算出的 π 的8位可靠數字，不但在當時是最精密的圓周率，而且保持世界紀錄九百多年。以至於有數學史家提議將這一結果命名為“祖率”。

　　這一結果是如何獲得的呢？追根溯源，正是基於對劉徽割圓術的繼承與發展，祖衝之才能得到這一非凡的成果。因而當我們稱頌祖衝之的功績時，不要忘記他的成就的取得是因為他站在數學偉人劉徽的肩膀上的緣故。後人曾推算若要單純地通過計算圓內接多邊形邊長的話，得到這一結果，需要算到圓內接正12288邊形，才能得到這樣精確度的值。祖衝之是否還使用了其它的巧妙辦法來簡化計算呢？這已經不得而知，因為記載其研究成果的著作《綴術》早已失傳了。這在中國數學發展史上是一件極令人痛惜的事。

	中國發行的祖衝之紀念郵票

　　祖衝之的這一研究成果享有世界聲譽：巴黎“發現宮”科學博物館的墻壁上著文介紹了祖衝之求得的圓周率，莫斯科大學禮堂的走廊上鑲嵌有祖衝之的大理石塑像，月球上有以祖衝之命名的環形山……

　　對於祖衝之的關於圓周率的第二點貢獻，即他選用兩個簡單的分數尤其是用密率來近似地表示 π 這一點，通常人們不會太注意。然而，實際上，後者在數學上有更重要的意義。

　　密率與 π 的近似程度很好，但形式上卻很簡單，並且很優美，只用到了數字1、3、5。數學史家梁宗巨教授驗證出：分母小于16604的一切分數中，沒有比密率更接近 π 的分數。在國外，祖衝之死後一千多年，西方人才獲得這一結果。

　　可見，密率的提出是一件很不簡單的事情。人們自然要追究他是採用什麼辦法得到這一結果的呢？他是用什麼辦法把圓周率從小數表示的近似值化為近似分數的呢？這一問題歷來為數學史家所關注。由於文獻的失傳，祖衝之的求法已不為人知。後人對此進行了各種猜測。

　　讓我們先看看國外歷史上的工作，希望能夠提供出一些信息。

　　1573年，德國人奧托得出這一結果。他是用阿基米德成果22／7與托勒密的結果377／120用類似于加成法“合成”的：(377-22) / (120-7) = 355/113。

　　1585年，荷蘭人安托尼茲用阿基米德的方法先求得：333/106 ＜ π ＜ 377/120，用兩者作為 π 的母近似值，分子、分母各取平均，通過加成法獲得結果：3 (15+17)/(106+120) = 355/113。

　　兩個雖都得出了祖衝之密率，但使用方法都為偶合，無理由可言。

　　在日本，十七世紀關孝和重要著作《括要算法》卷四中求圓周率時創立零約術，其實質就是用加成法來求近似分數的方法。他以3、4作為母近似值，連續加成六次得到祖衝之約率，加成一百十二次得到密率。其學生對這種按部就班的笨辦法作了改進，提出從相鄰的不足、過剩近似值就近加成的辦法，（實際上就是我們前面已經提到的加成法）這樣從3、4齣發，六次加成到約率，第七次出現25／8，就近與其緊鄰的22／7加成，得47／15，依次類推，只要加成23次就得到密率。

　　錢宗琮先生在《中國算學史》（1931年）中提出祖衝之採用了我們前面提到的由何承天首創的“調日法”或稱加權加成法。他設想了祖衝之求密率的過程：以徽率157／50，約率22／7為母近似值，並計算加成權數x=9，於是 (157 + 22，9) / (50+79) = 355/113，一舉得到密率。錢先生説：“衝之在承天后，用其術以造密率，亦意中事耳。”

　　另一種推測是：使用連分數法。

　　由於求二自然數的最大公約數的更相減損術遠在《九章算術》成書時代已流行，所以借助這一工具求近似分數應該是比較自然的。於是有人提出祖衝之可能是在求得盈 二數之後，再使用這個工具，將3.14159265表示成連分數，得到其漸近分數：3，22／7，333／106，355／113，102573／32650…

　　最後，取精確度很高但分子分母都較小的355／113作為圓周率的近似值。至於上面圓周率漸近分數的具體求法，這裡略掉了。你不妨利用我們前面介紹的方法自己求求看。英國李約瑟博士持這一觀點。他在《中國科學技術史》卷三第19章幾何編中論祖衝之的密率説：“密率的分數是一個連分數漸近數，因此是一個非凡的成就。”

　　我國再回過頭來看一下國外所取得的成果。

　　1150年，印度數學家婆什迦羅第二計算出 π= 3927/1250 = 3.1416。1424年，中亞細亞地區的天文學家、數學家卡西著《圓周論》，計算了3228＝805,306,368邊內接與外切正多邊形的周長，求出 π 值，他的結果是：

　　π＝3.14159265358979325

　　有十七位準確數字。這是國外第一次打破祖衝之的記錄。

　　16世紀的法國數學家韋達利用阿基米德的方法計算 π 近似值，用 6216正邊形，推算出精確到9位小數的 π 值。他所採用的仍然是阿基米德的方法，但韋達卻擁有比阿基米德更先進的工具：十進位置制。17世紀初，德國人魯道夫用了幾乎一生的時間鑽研這個問題。他也將新的十進制與早的阿基米德方法結合起來，但他不是從正六邊形開始並將其邊數翻番的，他是從正方形開始的，一直推導出了有262條邊的正多邊形，約4,610,000,000,000,000,000邊形！這樣，算出小數35位。為了紀念他的這一非凡成果，在德國圓周率 π 被稱為“魯道夫數”。但是，用幾何方法求其值，計算量很大，這樣算下去，窮數學家一生也改進不了多少。到魯道夫可以説已經登峰造極，古典方法已引導數學家們走得很遠，再向前推進，必須在方法上有所突破。

　　17世紀出現了數學分析，這銳利的工具使得許多初等數學束手無策的問題迎刃而解。 π 的計算歷史也隨之進入了一個新的階段。